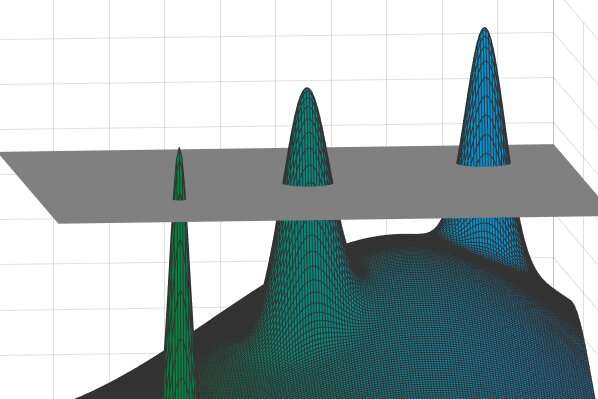
In alcuni casi, il diametro di ciascun picco sarà molto più piccolo delle distanze tra i diversi picchi. Pertanto, se si dovessero scegliere due punti qualsiasi su questo paesaggio tentacolare – cioè due possibili «soluzioni» – sarebbero o molto vicini (se provenissero dallo stesso picco) o molto distanti (se tratti da picchi diversi) . In altre parole, ci sarà un «vuoto» rivelatore in queste distanze – piccole o grandi, ma nessuna via di mezzo. Credito: David Jamarnik et al.
L’idea che alcuni problemi computazionali in matematica e informatica possano essere difficili non dovrebbe sorprendere. Esiste, infatti, un’intera classe di problemi per i quali si ritiene impossibile risolvere matematicamente. Al di sotto di questa categoria rientrano alcuni problemi «più facili» che non sono ben compresi – e potrebbero anche essere impossibili.
David Jamarnik, Professore di Ricerca Operativa presso la MIT Sloan School of Management e l’Institute for Data, Systems, and Society, concentra la sua attenzione su quest’ultima categoria di problemi meno studiati, che sono più rilevanti per il mondo di tutti i giorni perché coinvolgono A caso—Una caratteristica integrante dei sistemi naturali. Lui ei suoi colleghi hanno sviluppato un potente strumento per analizzare questi problemi chiamato proprietà del gap sovrapposto (o OGP). Gamarnik ha descritto la nuova metodologia in un recente documento di ricerca in Atti dell’Accademia Nazionale delle Scienze.
PNP
Cinquant’anni fa veniva formulato il problema più famoso dell’informatica teorica. P ≠ NP si chiede se ci sono problemi che coinvolgono enormi insiemi di dati la cui risposta può essere verificata in tempi relativamente brevi, ma che, anche se si lavora sui computer più veloci disponibili, richiederebbero tempi assurdamente lunghi per essere risolti.
La congettura P ≠ NP non è stata dimostrata, tuttavia la maggior parte degli informatici ritiene che molti problemi familiari, incluso, ad esempio, il problema del commesso viaggiatore rientrino in questa categoria incredibilmente difficile. La sfida nell’esempio del venditore è trovare il percorso più breve, in termini di distanza o tempo, attraverso N diverse città. L’attività è facilmente gestibile quando N = 4, perché ci sono solo sei possibili percorsi da considerare. Ma in 30 città ce ne sono più di 1030 modi possibili, e da lì i numeri salgono esponenzialmente. La difficoltà maggiore sta nella progettazione di un file algoritmo Risolve rapidamente il problema in tutti i casi, per tutti i valori interi di N., gli informatici sono fiduciosi, sulla base della teoria della complessità computazionale, che non esiste un tale algoritmo, confermando che P ≠ NP.
Ci sono molti altri esempi di tali problemi intrattabili. Supponiamo, ad esempio, di avere una tabella numerica enorme con migliaia di righe e migliaia di colonne. Riesci a trovare, tra tutte le possibili combinazioni, l’esatta disposizione di dieci righe e 10 colonne in modo tale che le loro cento voci abbiano la somma più alta raggiungibile? «Le chiamiamo attività di ottimizzazione, perché cerchi sempre di trovare il più grande o il migliore: la più grande somma di numeri, il percorso migliore attraverso le città, ecc.», afferma Jamarnik.
Gli informatici si sono resi conto da tempo che non è possibile creare un algoritmo veloce in grado, in tutti i casi, di risolvere i problemi con la stessa efficienza della saga del commesso viaggiatore. «È probabile che una cosa del genere sarebbe impossibile per ragioni ben note», osserva Jamarnik. «Ma nella vita reale, la natura non genera problemi da una prospettiva ostile. Non cerca di frustrarti con un problema ben selezionato e più impegnativo concepibile». In effetti, le persone di solito incontrano problemi in circostanze più casuali e meno gestite, e questi sono i problemi che l’Open Government Partnership mira ad affrontare.
Cime e valli
Per capire in cosa consiste l’Open Government Partnership, può essere utile vedere prima come è nata l’idea. Dagli anni ’70, i fisici hanno studiato lo spin glass, materiali che hanno proprietà sia dei liquidi che dei solidi che hanno comportamenti magnetici insoliti. La ricerca sugli occhiali rotanti ha dato origine a una teoria generale dei sistemi complessi relativi a problemi di fisica, matematica, informatica, scienza dei materiali e altri campi. (Questo lavoro ha fatto vincere a Giorgio Baresi il Premio Nobel per la Fisica 2021.)
Un problema confuso che i fisici hanno dovuto affrontare è il tentativo di prevedere lo stato energetico, in particolare le configurazioni a più bassa energia, di diverse strutture di vetro rotante. La situazione è talvolta rappresentata in un «paesaggio» di innumerevoli cime montuose separate da valli, dove l’obiettivo è individuare la vetta più alta. In questo caso, il picco più alto rappresenta effettivamente lo stato energetico più basso (sebbene si potrebbe invece capovolgere l’immagine e cercare il buco più profondo). Questo si rivela essere un problema di ottimizzazione simile nella forma al dilemma del commesso viaggiatore, Jamarnik spiega: «Hai questo enorme insieme di montagne e sembra che l’unico modo per trovare più in alto sia scalarle tutte»—un compito assurdo simile a trovare un ago in un pagliaio.
I fisici hanno dimostrato che puoi semplificare questa immagine e fare un passo verso una soluzione, tagliando le montagne a una certa altezza predeterminata e ignorando tutto al di sotto di quel livello di soglia. Lascerai quindi un gruppo di picchi prominenti sopra uno strato uniforme di nuvole, con ogni punto in quei picchi che rappresenta una potenziale soluzione al problema originale.
In un documento di ricerca del 2014, Jamarnik e colleghi notano qualcosa che in precedenza era stato trascurato. Si sono resi conto in alcuni casi che il diametro di ciascun picco sarebbe stato molto più piccolo delle distanze tra i diversi picchi. Pertanto, se si dovessero scegliere due punti qualsiasi su questo paesaggio tentacolare – cioè due possibili «soluzioni» – sarebbero o molto vicini (se provenissero dallo stesso picco) o molto distanti (se tratti da picchi diversi) . In altre parole, ci sarà un «vuoto» rivelatore in queste distanze – piccole o grandi, ma nessuna via di mezzo. Jamarnik e colleghi hanno suggerito che il sistema in questo caso è caratterizzato da OGP.
«Abbiamo scoperto che tutti i problemi noti di natura casuale computazionalmente difficile hanno una versione di questa proprietà», ovvero il diametro della montagna nel modello schematico è molto più piccolo della distanza tra le montagne, afferma Jamarnik. «Questo fornisce una misura più accurata della robustezza dell’algoritmo».
Svelare i segreti della complessità dell’algoritmo
L’avvento dell’OGP potrebbe aiutare i ricercatori a valutare la difficoltà di creare algoritmi veloci per affrontare problemi specifici. Ha già consentito loro di «matematicamente [and] Ha fortemente escluso un’ampia classe di algoritmi come potenziali concorrenti», afferma Jamarnik. Abbiamo appreso, in particolare, che gli algoritmi stabili – quelli il cui output non cambierà molto se l’input cambia solo un po’ – non riusciranno a risolvere questo tipo di problema di ottimizzazione. «Questo risultato negativo si applica non solo ai computer classici, ma anche ai computer quantistici, e in particolare ai cosiddetti «algoritmi di ottimizzazione dell’approssimazione quantistica» (QAOA), che alcuni ricercatori speravano risolvessero gli stessi problemi di ottimizzazione. Ora visti i risultati di Jamarnik e i risultati dei coautori, queste speranze sono mitigate dal riconoscimento che saranno necessari molti livelli di operazioni per il successo degli algoritmi di tipo QAOA, il che può essere tecnicamente impegnativo.
«Se questa è una buona o una cattiva notizia dipende dal tuo punto di vista», dice. «Penso che sia una buona notizia nel senso che ci aiuta a svelare i segreti della complessità algoritmica e migliora la nostra conoscenza di cosa è nel regno della probabilità e cosa non lo è. È una cattiva notizia nel senso che ci dice che questi problemi sono difficile, anche se la natura li produce, e anche se vengono generati casualmente”. Aggiunge che la notizia non è davvero sorprendente. «Molti di noi se lo aspettavano da sempre, ma ora abbiamo una base molto più solida per fare questa affermazione».
Ciò lascia ancora i ricercatori lontani anni luce dal poter dimostrare che non esistono algoritmi veloci in grado di risolvere questi problemi di ottimizzazione in impostazioni casuali. Avere tali prove fornirebbe una risposta definitiva al problema P NP. Dice: «Se riusciamo a dimostrare che non possiamo avere un algoritmo che funzioni la maggior parte del tempo, questo ci dice che non possiamo assolutamente avere un algoritmo che funzioni sempre».
Prevedere quanto tempo ci vorrà prima che il problema PNP sia risolto sembra essere di per sé un problema intrattabile. Probabilmente ci saranno molte vette da scalare e valli da attraversare, prima che i ricercatori ottengano una prospettiva più chiara della situazione.
David Jamarnik, La proprietà Nested Gap: una barriera topologica all’ottimizzazione delle strutture stocastiche, Atti dell’Accademia Nazionale delle Scienze (2021). DOI: 10.1073/pnas.2108492118
Introduzione di
Istituto di Tecnologia del Massachussetts
la citazione: il ricercatore sviluppa un nuovo strumento per comprendere problemi computazionali difficili e apparentemente intrattabili (2022, 10 gennaio) Estratto l’11 gennaio 2022 da https://phys.org/news/2022-01-tool-hard-problems-intractable.html
Questo documento è soggetto a copyright. Nonostante qualsiasi correttezza commerciale a fini di studio o ricerca privati, nessuna parte può essere riprodotta senza autorizzazione scritta. Il contenuto è fornito a solo scopo informativo.






More Stories
Los legionarios realizan dos cruceros separados vinculados a esta característica especial de lujo: informe
La supernova vista por primera vez en 1181 libera filamentos brillantes
SpaceX lanza 20 satélites de Internet Starlink desde California el 30 de octubre